ĐỀ MẪU CĨ ĐÁP ÁN

ƠN TẬP KIẾN THỨC
TỐN 12
Thời gian làm bài: 40 phút (Không kể thời gian giao đề)
-------------------------

Họ tên thí sinh: .................................................................
Số báo danh: ......................................................................
Mã Đề: 023.
Câu 1. Diện tích xung quanh của khối nón có chiều cao đường sinh l và bán kính đáy là
A. π r 2 h .
B. πrl.
C. π r 2 l .
D. π r h.
Đáp án đúng: B
Câu 2. Đồ thị của hàm số nào sau đây khơng cắt trục hồnh?
A.

.

B.

.

C.
.
D.
.
Đáp án đúng: A
Giải thích chi tiết: Đồ thị của hàm số nào sau đây khơng cắt trục hồnh?

A.
. B.
Lời giải
Xét các phương trình sau:

. C.

. D.

.

cắt trục hồnh tại
cắt trục hồnh tại

B.

.

Câu 5. Bất phương trình
A. .
Đáp án đúng: D
Câu 6. Đồ thị hàm số

và , loại phương án C

không cắt trục hoành, chọn phương án D

Câu 3. Gọi , là hai nghiệm phức của phương trình
A.
.

B.
.
Đáp án đúng: D
Câu 4. . Hàm số y = x4 + 2x2 - 1 nghịch biến trên :
A.
.
Đáp án đúng: A

, loại phương án A

, loại phương án B

cắt trục hồnh tại
(vơ nghiệm)

và tiếp xúc trục hồnh tại

. Giá trị
C.

C.

.

.

bằng
D. .

D.


.

có bao nhiêu nghiệm ngun?
B. Vơ số.

C. .

D.

.

có tâm đối xứng là:
1


A. Khơng có tâm đối xứng.

B.

C.
.
Đáp án đúng: C

D.

Giải thích chi tiết: Đồ thị hàm số y =
A.

.


. B.

.

có tâm đối xứng là:

.

C.
. D. Khơng có tâm đối xứng
Đáp án: A
Câu 7.
Trong không gian với hệ tọa độ

, cho hai điểm

. Mặt cầu đường kính

có phương trình là
A.

.

B.

.

C.


.

D.
Đáp án đúng: B

.

Giải thích chi tiết: Trong khơng gian với hệ tọa độ
cầu đường kính

, cho hai điểm

. Mặt

có phương trình là

A.

.

B.

.

C.
Lời giải

.

D.


.

Gọi

là trung điểm

ta có

là tâm mặt cầu.

Bán kính
Vậy phương trình mặt cầu cần tìm là

.

Câu 8. Bên trong bồn chứa nước hình trụ có đường kính đáy bằng chiều cao và bằng
bồn chứa đó bằng
A.

.

B.

. Thể tích thực của

.
2



C.
Đáp án đúng: B

.

D.

.

Câu 9. Cho hàm số
. Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng là
.
B. Đồ thị hàm số có tiệm cận ngang là
C. Đồ thị hàm số có tiệm cận đứng là

.

D. Đồ thị hàm số có tiệm cận ngang là
Đáp án đúng: B
Câu 10. Trong không gian với hệ tọa độ
cho các điểm
(không trùng
lần lượt thay đổi trên các
trục
và ln thỏa mãn điều kiện: tỉ số giữa diện tích của tam giác
và thể tích khối tứ diện
bằng Biết rằng mặt phẳng
A.
B.

Đáp án đúng: D
Giải thích chi tiết:
Lời giải.

ln tiếp xúc với một mặt cầu cố định, bán kính của mặt cầu đó bằng
C.
D.

Cách 1. Ta có

mà
Vậy mặt phẳng

Cách 2. Giả sử

ln tiếp xúc mặt cầu tâm
(với

có bán kính

.

).

Lại có

3


Theo đề, ta có


Vậy mặt phẳng
Câu 11.
Điểm

ln tiếp xúc với mặt cầu tâm

trong hình vẽ biểu diễn số phức

A.
.
Đáp án đúng: D

B.

Giải thích chi tiết: Điểm

A.
Lời giải
Điểm

bán kính

. B.

.

C.

D.


trong hình vẽ biểu diễn số phức

.

C.

.

D.

trong hình vẽ biểu diễn số phức

Câu 12. Đồ thị hàm số

.

có các đường tiệm cận đứng, tiệm cận ngang lần lượt là

A.

B.

C.
Đáp án đúng: C
Câu 13. Thể tích khối tứ diện đều cạnh
A.
.
Đáp án đúng: A


D.
là

B.

Câu 14. Cho
A.
.
Đáp án đúng: A

và

.

C.

. Tính giá trị của biểu thức
B.
.
C.

.

D.

A.

.

.

.

D.

Giải thích chi tiết:
Câu 15.
Cho

.

.

.

là số thực dương, tính tích phân
.

theo
B.

.
.
4


C.
Đáp án đúng: A

.


D.

Giải thích chi tiết: Vì
Câu 16.

nên

Lắp ghép hai khối đa diện

để tạo thành khối đa diện

tứ giác đều có tất cả các cạnh bằng
trùng với một mặt của
A.
Đáp án đúng: A

,

Câu 17. Trong không gian với hệ tọa độ
, , (khác gốc

A.

như hình vẽ. Hỏi khối da diện

, gọi
) sao cho

có tất cả bao nhiêu mặt?
D.


là mặt phẳng qua

và cắt các trục

là trọng tâm tam giác

.

là khối chóp
sao cho một mặt của

C.

.

C.
Đáp án đúng: D
Giải thích chi tiết:
Lời giải

, trong đó

là khối tứ diện đều cạnh

B.

lần lượt tại các điểm
phương trình


.

,

. Khi đó mặt phẳng

B.

.

D.

.

,
có

Gọi

Ta có
Vậy mặt phẳng
Câu 18.

có phương trình

Cho hình chóp tứ giác đều
. Hình hộp có đáy là
tích khối chóp

,


.
có tâm đáy là
, đáy kia là

là thể tích khối hộp

. Gọi
với

lần lượt là trung điểm của
là trung điểm của

. Gọi

là thể

. Tính tỉ số

5


Ⓐ.

. Ⓑ. . Ⓒ. . Ⓓ.
A.
Đáp án đúng: C

.
B.


C.

Câu 19. Tìm số nghiệm của phương trình
A. .
B. .
Đáp án đúng: B

D.

trên
C. .

Giải thích chi tiết: Tìm số nghiệm của phương trình

D. .
trên

A. . B. . C. . D. .
Lời giải
Ta có

mà

Mặt khác
nên ta có
Vậy phương trình có 4 nghiệm.
Câu 20. Trong không gian cho đường thẳng
A. .
B. .

Đáp án đúng: D

nên
.

và điểm

. Qua
C. .

Câu 21. Thể tích của khối hộp chữ nhật có ba kích thước
A.
Đáp án đúng: C

B.

Câu 22. Tập nghiệm của bất phương trình
A.
C.
Đáp án đúng: B

.

có mấy đường thẳng vng góc với
D. Vơ số.

?

bằng
C.


D.

là
B.
D.

Câu 23. Một hình nón có thiết diện qua trục là một tam giác vng cân có cạnh góc vng bằng
tích xung quanh của hình nón.

Tính diện
6


A.

.

B.

C.
.
Đáp án đúng: C

.

D.

.


Câu 24. Cho hàm số
có đồ thị là
. Gọi
là tọa độ trên
tiệm cận đứng bằng lần khoảng cách M tới tiệm cận ngang. Tọa độ điểm

là

thỏa mãn khoảng cách từ M tới

A.
B.
C.
D.
Đáp án đúng: D
Câu 25.
Giá trị lớn nhất của hàm số

trên đoạn

A.

là:

B.

C.
Đáp án đúng: B
Câu 26.


D.

Trong khơng gian với hệ tọa độ

cho các vec tơ

Tìm tọa độ của vec

tơ
A.
C.
Đáp án đúng: C

.

B.

.

D.

Giải thích chi tiết: Trong khơng gian với hệ tọa độ

.
.

cho các vec tơ

Tìm tọa


độ của vec tơ
A.
Lời giải
Ta có

. B.

. C.
và

. D.

.

. Suy ra

2 x+ 5
. Khẳng định nào sau đây đúng?
3 x−1
1
2
A. Đồ thị hàm số có tiệm cận ngang là x=
B. Đồ thị hàm số có tiệm cận đứng là x=
3
3
1
2
C. Đồ thị hàm số có tiệm cận ngang là y=
D. Đồ thị hàm số có tiệm cận ngang là y=
3

3
Đáp án đúng: D

Câu 27. Cho hàm số y=

7


Câu 28. ~(Mã 101 - năm 2021) Trên đoạn
A.
.
Đáp án đúng: C

B.

Câu 29. Cho tích phân

.

B.

,

C.

.

D.

,


.

,

Đổi cận:

đạt giá trị lớn nhất tại điểm

. Nếu đổi biến số

A.
.
Đáp án đúng: B
Giải thích chi tiết:
Lời giải
Đặt

, hàm số

C.

.

thì:

.

D.


.

.

,

.

.
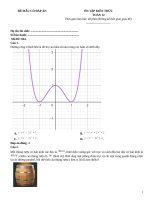
Câu 30. Biết rằng đồ thị của hàm số y=a x +b x +cx +d có hai điểm cực trị là ( 0 ; 0 )và ( 1 ; 1 ). Các hệ số a ,b ,c ,d
lần lượt là
A. −2 ;3 ;0 ;0 .
B. −2 ;0 ;0 ;3.
C. 0 ;0 ;−2 ;3.
D. −2 ;0 ;3 ;0 .
Đáp án đúng: A
Giải thích chi tiết: [Mức độ 2] Biết rằng đồ thị của hàm số y=a x3 +b x 2 +cx +d có hai điểm cực trị là ( 0 ; 0 )và
( 1 ; 1 ). Các hệ số a ,b ,c ,d lần lượt là
A. −2 ;0 ;3 ;0 . B. −2 ;3 ;0 ;0 . C. −2 ;0 ;0 ;3. D. 0 ;0 ;−2 ;3.
Lời giải
y ′ =3 a x 2 +2 bx+ c=0( ¿ ) .
3

2

Đồ thị của hàm số đã cho có 2 điểm cực trị là ( 0 ; 0 )và ( 1 ; 1 ).

{ {
′


y ( 0 )=0
c=0
a=−2
′
⇔ y ( 1 )=0 ⇔ 3 a+ 2b +c=0 ⇒ b=3 .
d=0
y ( 0 )=0
c=d=0
a+b+c +d =1
y ( 1 )=1

{

Vậy các hệ số a ,b ,c ,d lần lượt là −2 ;3 ;0 ;0 .
Câu 31.
Tập xác định của hàm số
A.

.

C.
.
Đáp án đúng: B
Giải thích chi tiết: Hàm số

là
B.

.


D.

.

xác định khi:

.
8


Vậy tập xác định của hàm số đã cho là:
Câu 32. Nếu

.

thì

A. .
Đáp án đúng: D

bằng
B.

.

C. .

Câu 33. Cho hình lăng trụ
A. Nếu


là hình chữ nhật.

là hình hộp khi và chỉ khi

C. Nếu

là hình chữ nhật.

là hình hộp thì

D.
Đáp án đúng: D
Câu 34.

.

. Phát biểu nào sau đây là đúng?
là hình hộp thì

B.

D.

.

là hình hộp khi và chỉ khi

là hình bình hành.

Khi tăng độ dài cạnh đáy của một khối chóp tam giác đều lên


lần và giảm chiều cao của hình chóp đó đi

lần thì thể tích khối chóp thay đổi như thể nào?
A. Tăng lên

lần.

B. Tăng lên

C. Giảm đi
Đáp án đúng: D

lần.

D. Khơng thay đổi.

Giải thích chi tiết: Ta có thể tích hình chóp là:
Giả sử cạnh đáy bằng
Nếu cạnh đáy tăng lên

.

thì diện tích đáy
lần, tức là

lần.

.
thì diện tích đáy bằng


và chiều cao

lần, tức bằng
thì thể tích khối chóp bằng
Do đó thể tích khối chóp khơng thay đổi.
Câu 35.
Nguyên hàm
A.
C.
Đáp án đúng: B
Giải thích chi tiết: Với

trên khoảng

giảm đi

.

là

.

B.

.

.

D.


.

, ta có

.
----HẾT--9


10