ĐỀ MẪU CĨ ĐÁP ÁN

ƠN TẬP KIẾN THỨC
TỐN 12
Thời gian làm bài: 40 phút (Không kể thời gian giao đề)
-------------------------

Họ tên thí sinh: .................................................................
Số báo danh: ......................................................................
Mã Đề: 029.
Câu 1. Cho

với

là các số nguyên và

. Tính

.
A.
.
Đáp án đúng: B
Giải thích chi tiết: Ta có

Tính
Đổi cận:

B.

.

C.

. Đặt

.

D.

.

.

. Khi đó

.

Vậy

.

Câu 2. Thể tích vật thể trịn xoay khi quay hình phẳng giới hạn bởi các đường
quanh trục ox là:
A.
B.
C.
D.
Đáp án đúng: D
Giải thích chi tiết: Thể tích vật thể trịn xoay khi quay hình phẳng giới hạn bởi các đường
quanh trục ox là:
A.

B.
C.
Hướng dẫn giải

D.

Theo cơng thức ta có thể tích của khối trịn xoay cần tính là:
Câu 3. Trong khơng gian với hệ tọa độ
và điểm

, cho ba mặt phẳng
nằm giữa hai mặt phẳng

luôn đi qua
và luôn tiếp xúc với hai mặt phẳng
là hình trịn có diện tích lớn nhất thì
bằng

Khi khối cầu

Mặt cầu

di động có tâm

cắt mặt phẳng

theo thiết diện
1



A.
Đáp án đúng: A
Giải thích chi tiết:
Lời giải.

B.

Ta tính được

C.

Ta tìm được mặt phẳng cách đều cả hai mặt phẳng

Gọi bán kính của mặt cầu

là

Vì mặt cầu

Theo đề, ta có

Suy ra

Ta có

mặt cầu

Khối cầu

cắt mặt phẳng


với mặt phẳng

ln tiếp xúc với hai mặt phẳng

thuộc mặt cầu

B.

đi qua
C.

,

. D.

.

D.

đồng

.

, cho hai điểm

và đường thẳng
đi qua

,


vng góc

.

có vectơ chỉ phương

;

là một vectơ chỉ phương của đường thẳng

.

.

Mặt khác,

.

Nên

Xét

.

vng góc với đường thẳng

. Gọi
là một vectơ chỉ phương của đường thẳng
đồng thời cách điểm

một khoảng nhỏ nhất. Giá trị
là

. C.

là tiếp điểm của mặt cầu

và đường thẳng

.

Giải thích chi tiết: Trong khơng gian

Theo đề,

và bán kính

theo thiết diện là hình trịn có diện tích lớn nhất khi

, cho hai điểm

A. .
Đáp án đúng: C

Đường thẳng

có tâm

tiếp xúc với mặt phẳng


Gọi
là một vectơ chỉ phương của đường thẳng
thời cách điểm
một khoảng nhỏ nhất. Giá trị
là

với đường thẳng

là

Khi đó

Câu 4. Trong khơng gian

A. . B.
Lời giải

D.

.

.
2


.
Bảng biến thiên

Vậy khoảng cách từ
Câu 5.

Trong mặt phẳng

đến

nhỏ nhất khi

, số phức

A. Điểm .
Đáp án đúng: B

được biểu diễn bởi điểm nào trong các điểm ở hình vẽ dưới đây?

B. Điểm

Giải thích chi tiết: Trong mặt phẳng
Câu 6.

Tập xác định của

A.
.
Đáp án đúng: B

.

C. Điểm

, số phức


.

D. Điểm

.

được biểu diễn bởi điểm có tọa độ

.

là
B.

.

Câu 7. Cho khối trụ có bán kính đáy
A.
.
Đáp án đúng: D

.

B.

C.

và chiều cao
.

.


D.

.

. Tính thể tích khối trụ đó.
C.

Câu 8. Giá trị cịn lại của một chiếc xe mua mới theo thời gian

.

D.

.

được xác định bởi cơng thức:

,

trong đó
được tính bằng tỷ đồng và tính bằng năm. Sau ít nhất bao nhiêu năm kể từ thời điểm mua xe
giá trị chiếc xe đó cịn lại dưới
triệu đồng?
A. .
Đáp án đúng: C

B.

.


C. .

D.

.
3


Câu 9.
Hỏi

có

tất

cả

bao

nhiêu

giá

trị

nguyên

của


tham

số

đồng biến trên khoảng
A.
.
Đáp án đúng: C

B.

Câu 10. Cho số phức

.

A.
.
Đáp án đúng: C

B.

.

D.

. Số phức liên hợp của số phức
.

hàm


số

hàm

số

?

C.

thỏa mãn

để

C.

.

.
là?

D.

Giải thích chi tiết: Ta có:

.

.

.

Câu 11. Các số thực
A.

,

thỏa mãn

là

.

B.

.

C.
.
D.
.
Đáp án đúng: D
Câu 12. Quả bóng được dùng thi đấu tại các giải bóng đá Việt Nam tổ chức có chu vi thiết diện qua tâm là
68,5 ( cm ). Quả bóng được ghép nối các miếng da hình lục giác đều màu trắng mỗi miếng có diện tích
49,83 ( c m2 ) và 5 miếng da hình ngũ giác đều màu đen có, mỗi miếng có diện tích 50,11 ( c m2) . Hỏi cần ít nhất
bao nhiêu miếng da hình lục giác để làm quả bóng trên?
A. ≈ 25 (miếng da).
B. ≈ 35(miếng da).
C. ≈ 30 (miếng da).
D. ≈ 40 (miếng da).
Đáp án đúng: A
Câu 13. Cho các số phức

đó:
A.
.
Đáp án đúng: C

thoả mãn
B.

. Gọi
.

C.

Giải thích chi tiết: Gọi

.

nhỏ nhất. Khi
D.

.

lần lượt là điểm biểu diễn của các số phức

Từ giả thiết

là đường trung trực của đoạn

Ta có :
Gọi


là số phức thoả mãn

.

.

.
. Do đó

là hình chiếu của

lên

.

Khi đó

Tọa độ điểm

là nghiệm của hệ phương trình

.
4


Vậy

.


Câu 14.

bằng:

A.

.

B.

.

C.
.
Đáp án đúng: D

D.

.

Giải thích chi tiết:
E.

.

bằng:
F.

.


G.

Câu 15. Cho hình lăng trụ tam giác
,

. H.

.

, biết hình chóp

. Tính thể tích khối lăng trụ

A.
.
Đáp án đúng: A

B.

theo

.

C.

Giải thích chi tiết: Cho hình lăng trụ tam giác
cạnh bằng

,


Gọi
,

,
là trung điểm của

C.

,

, biết hình chóp

là hình thoi. Suy ra

Vậy thể tích khối lăng trụ là

.

là hình chóp tam giác đều

theo

.

.

là tâm đường trịn ngoại tiếp tam giác

. Mà


vng tại

D.

D.

,

là trung điểm của

.

Ta có

Tam giác

.

.
.

. Tính thể tích khối lăng trụ

A.
. B.
.
Lời giải
FB tác giả: Hua Vu Hai

là hình chóp tam giác đều cạnh bằng


,

suy ra

hay

.
, có

.
.
5


Câu 16. Rút gọn biểu thức
A.
Đáp án đúng: B

ta được kết quả bằng
B.

C.

Giải thích chi tiết: Rút gọn biểu thức
A.
Lời giải

B.


C.

ta được kết quả bằng

D.

Theo tính chất lũy thừa

ta có

Câu 17. Cho khối lập phương có cạnh bằng
A. 64.
Đáp án đúng: D
Câu 18.

B.

. Diện tích tồn phần của khối lập phương đã cho bằng

.

C.

Tính thể tích khối lập phương có cạnh bằng
A.

.

C.
.

Đáp án đúng: D
Câu 19. Tích phân
A. .
Đáp án đúng: D
Câu 20.
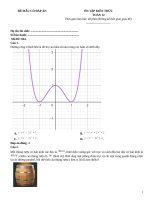
Cho hàm số
hình vẽ bên.

Gọi

D.

.

D. 96.

.
B.

.

D.

.

bằng:
B.

.


và hàm số

C.

.

D.

.

có đồ thị là các đường cong như

là diện tích của hình phẳng được tơ đậm. Khẳng định nào sau đây đúng?

6


A.

B.

.

C.
.
Đáp án đúng: B

D.

.


Giải thích chi tiết: Cho hàm số
đường cong như hình vẽ bên.

và hàm số

Gọi

.

có đồ thị là các

là diện tích của hình phẳng được tơ đậm. Khẳng định nào sau đây đúng?

A.
Lời giải

. B.

. C.

. D.

.

Từ đồ thị ta thấy đồ thị hàm hàm số

đi qua các điểm

tại


,

và đạt cực trị

.

Từ đồ thị ta lại thấy đồ thị hàm số

đi qua các điểm

,

và

.
Diện tích hình phẳng được tô đậm là

.
Câu 21. Trong không gian với hệ tọa độ

, cho bốn véc tơ

. Trong các bộ số sau, bộ số nào là tọa độ của

và

?
7



A.
.
Đáp án đúng: B
Câu 22. Cho

,

B.
,

với

,

A.

,

với

,

.

là các số thực dương khác ,

. Khẳng định nào sau đây là sai ?

.


Biểu thức ở đáp án C chỉ đúng khi bổ sung thêm điều kiện
Câu 23. Có tất cả bao nhiêu giá trị nguyên của

.

để phương trình

B.

C.

Câu 24. Phương trình
C.
Đáp án đúng: C

.

.

. D.

A. .
Đáp án đúng: A

.

. Khẳng định nào sau đây là sai?

D.

,

D.

B.

. B.

A.

.

là các số thực dương khác ,

.

Giải thích chi tiết: Cho

C.
Lời giải

C.

.

C.
Đáp án đúng: D

A.


.

có 3 nghiệm phân biệt.

.

D.

.

tương đương với phương trình nào dưới đây?

.

B.

.

.

D.

.

Câu 25. Cho số phức

. Khẳng định nào sau đây là khẳng định sai?

A. là một số thuần ảo.
C.

.
Đáp án đúng: D

B.
D.

Giải thích chi tiết: Cho số phức

.
có phần ảo bằng 0.

. Khẳng định nào sau đây là khẳng định sai?

A. có phần ảo bằng 0.
B.
.
C.
.
D. là một số thuần ảo.
Hướng dẫn giải
. Do đó A sai.
Vậy chọn đáp án A.
Câu 26. . Cho khối hộp chữ nhật có ba kích thước 3; 4; 5. Thể tích của khối hộp đã cho bằng
A.
Đáp án đúng: D

B.

C.


D.

8


Câu 27. Trong không gian

, cho véctơ

A.
.
Đáp án đúng: C
Câu 28.

B.

.

Trong không gian với hệ tọa độ
điểm

sao cho

điểm

A.
.
Đáp án đúng: A

. Tọa độ của véctơ


B.

C.

.

D.

, cho ba điểm

,

là

đỉnh của một hình bình hành là

.

C.

B. Vơ số

.

,

.

D.


Câu 29. Tập nghiệm của bất phương trình
A.
Đáp án đúng: C

là

C.

.

có tất cả bao nhiêu số nguyên?
C.

D.

Giải thích chi tiết: Tập nghiệm của bất phương trình
số ngun?
A.
B.
Lời giải

, số

có tất cả bao nhiêu

D. Vơ số

Ta


có

.
.
Vậy tập nghiệm của bất phương trình có giá trị ngun.
Câu 30. Ơng Tốn gửi ngân hàng 150 triệu đồng với lãi suất 0,8%/tháng, sau mỗi tháng tiền lãi được nhập vào
vốn. Hỏi sau một năm số tiền lãi ơng Tốn thu được là bao nhiêu? (làm trịn đến nghìn đồng)
A. 15.051.000 đồng.
B. 165.051.000 đồng.
C. 165.050.000 đồng.
D. 15.050.000 đồng.
Đáp án đúng: A
Giải thích chi tiết:
+) Sau một năm số tiền cả vốn lẫn lãi của ơng Tốn là:

triệu đồng.

+) Vậy tiền lãi ơng Tốn thu được sau một năm là:
Câu 31.
Cho hai đường tròn

và

cắt nhau tại hai điểm

triệu đồng.
và

sao cho


là một đường kính của đường

trịn
Gọi
là diện tích hình phẳng giới hạn bởi hai đường trịn (ở ngồi đường trịn lớn, phần gạch chéo
như hình vẽ). Quay hình
quanh trục
ta được một khối trịn xoay. Thể tích của khối trịn xoay được tạo
thành bằng
9


A.
Đáp án đúng: A
Giải thích chi tiết:
Lời giải.

B.

Ta có:

và

Vì

suy ra
vng tại

C.


D.

nên ta có

Cách 1. (Dùng cơng thức thuần túy)
• Thể tích khối nón đỉnh

bán kính đáy

là:

• Thể tích chỏm cầu (hình cầu lớn) có

là:

• Thể tích khối nón đỉnh

là:

bán kính đáy

• Thể tích chỏm cầu (hình cầu nhỏ) có

là:

Suy ra thể tích cần tìm
Cách 2. (Dùng tích phân) Dễ dàng viết được phương trình

và hai phương trình đường trịn là


và
Thể tích cần tìm
10


Câu 32. Cho hàm số

(

là các tham số nguyên). Có tât cả bao nhiêu bộ số

sao cho
A. .
Đáp án đúng: C

B.

.

C.

.

D.

.

Giải thích chi tiết: Ta có
.
Mặt khác ta lại có

.
.
Dấu bằng xảy ra khi

.

Khi đó
.
Do

là các tham số nguyên nên

và

.

Vậy có tât cả

bộ số

sao cho

Câu 33. Cho hàm số

.

xác định và liên tục trên ℝ thỏa mãn đồng thời các điều kiện sau
và

độ


. Phương trình tiếp tuyến của đồ thị tại điểm có hồnh

là
A.

B.

C.
Đáp án đúng: D

D.

Giải thích chi tiết: Ta có:

Mặt khác

Ta có:

Phương trình tiếp tuyến của đồ thị tại điểm có hồnh độ

là:
11


.
Câu 34. Cho hàm số

. Tìm tập hợp tất cả các giá trị của tham số thực


để hàm số đồng biến trên

.
A.
.
Đáp án đúng: B
Câu 35. : Đồ thị hàm số y=
A. 1
Đáp án đúng: C

B.

.

C.

.

D.

.

2

x −1
có số đường tiệm cận là:
2
x + 2 x −3
B. 0
C. 2


D. 3

----HẾT---

12